数组
型, dimension(上限: 下限)::命名斐波那契数列
a0 = 1, a1 = 1, an+1 = an + an-1
program fb
implicit none
integer, dimension(0: 10) :: a
integer :: i
a(0) = 1.0
a(1) = 1.0
do i = 1, 9
a(i+1) = a(i) + a(i-1)
end do
print '(1x,11i4)', (a(i), i = 0, 10)
print *, 'press any key to continue'
read *,
stop
end 1 1 2 3 5 8 13 21 34 55 89
press any key to continue平均值与标准差
program name
implicit none
integer :: i, n
real :: s, x, mu, s2, sigma
real, dimension(100) :: a
print *, 'n = '
read *, n
! 输入n个值
do i = 1, n
print '(1x, a2, i2, a2)','a(',i,')='
read *, a(i)
end do
! 计算平均数
s = 0.0
do i = 1, n
s = s + a(i)
end do
mu = s / n
! 计算标准差
x=0.0
do i = 1, n
x = x + (a(i) - mu)**2
end do
s2 = x / (real(n))
sigma = sqrt(s2)
print *, 'mean', mu
print *, 'standard deviation', sigma
print *, 'press any key to continue'
read *,
stop
end program name n =
6
a( 1)=
1513654156
a( 2)=
514514551
a( 3)=
513513
a( 4)=
1235413513
a( 5)=
61351438979845
a( 6)=
13212131
mean 1.02257855E+13
standard deviation 2.28640885E+13
press any key to continue最小二乘法
program abc
implicit none
integer :: i, n
real :: sx, sy, mux, muy, s1, s2, alpha, beta
integer, dimension(100) :: x, y
print *, 'n = '
read *, n
! 对于x输入n个值
do i = 1, n
print '(1x, a2, i2, a2)','x(',i,')='
read *, x(i)
end do
! 对于y输入n个值
do i = 1, n
print '(1x, a2, i2, a2)','y(',i,')='
read *, y(i)
end do
! 计算x平均数
sx = 0.0
do i = 1, n
sx = sx + x(i)
end do
mux = sx / n
! 计算y平均数
sy = 0.0
do i = 1, n
sy = sy + y(i)
end do
muy = sy / n
! 计算系数
s1 = 0.0
do i = 1, n
s1 = s1 + (x(i) - mux) * (y(i) - muy)
end do
s2 = 0.0
do i = 1, n
s2 = s2 + (x(i) - mux) ** 2
end do
beta = s1 / s2
alpha = muy - beta * mux
! 输出结果
print *, 'mean x = ', mux
print *, 'mean y = ', muy
print '(1x, a2, f7.3, a1, f7.3, a1)', 'y=', alpha, '+', beta, 'x'
print *,'press any key to continue'
read *,
stop
end n =
3
x( 1)=
1
x( 2)=
2
x( 3)=
3
y( 1)=
1
y( 2)=
3
y( 3)=
2
mean x = 2.00000000
mean y = 2.00000000
y= 1.000+ 0.500x
press any key to continue向量
当a和b同为n维向量时,有
| 写法 | 意义 |
|---|---|
| a + b | ai + bi (i = 1, ..., n) |
| a - b | ai - bi (i = 1, ..., n) |
| a * b | ai * bi (i = 1, ..., n) |
| a / b | ai / bi (i = 1, ..., n) |
| a ^ b | ai ^ bi (i = 1, ..., n) |
| dot_product(a, b) | 点积 |
内积
program vector
implicit none
real, dimension(4) :: a, b, c
real :: s
print *, 'a = '
read *, a
print *, 'b = '
read *, b
c = a * b
s = dot_product(a, b)
print '(1x, 5f15.0)', c
print *, 'dot_product(a, b) =', s
print *, 'press any key to continue'
read *,
stop
end a =
10156,457845,16119,4795
b =
14545,16197,1616,4641
147719024. 7415715328. 26048304. 22253596.
dot_product(a, b) = 7.61173658E+09
press any key to continue外积(三维)
program abc
implicit none
integer :: i
integer, dimension(3) :: a, b
integer, dimension(1, 3) :: c
do i = 1, 3
print '(1x, a2, i1, a2)', 'a(', i, ')='
read *, a(i)
end do
do i = 1, 3
print '(1x, a2, i1, a2)', 'b(', i, ')='
read *, b(i)
end do
c = reshape((/a(2)*b(3) - a(3)*b(2), a(3)*b(1) - a(1)*b(3), a(1)*b(2) - a(2)*b(1)/), (/1, 3/))
print *, c
print *,'press any key to continue'
read *,
stop
end a(1)=
3
a(2)=
5
a(3)=
8
b(1)=
2
b(2)=
2
b(3)=
6
14 -2 -4
press any key to continue矩阵
当符合矩阵各运算的定义时,有
| 写法 | 意义 |
|---|---|
| a + b | a + b(相加) |
| a - b | a - b(相减) |
| alpha*a | αa(标量倍) |
| matmul(a, b) | ab(矩阵乘法) |
| transpose(a) | aT(转置) |
| a * b | 元素之积 |
| a / b | 元素之商 |
| a**n | 元素的n次方 |
使用reshape表示单位矩阵(3×3)
program matrix_e
implicit none
integer :: i
integer, dimension(3, 3) :: p = reshape((/1, (0, i = 1, 3), 1, (0, i = 1, 3), 1/), (/3, 3/))
!reshape(/(数或变量, 变量 = 起始值, 终止值, 递增值), (/行数, 列数/)/)
print *, 'p = '
print '(1x, 3i5)', p
print*, 'press any key to continue'
read*,
stop
end p =
1 0 0
0 1 0
0 0 1
press any key to continue使用sum求行之和,列之和与总和
program jhjh
implicit none
integer::i,j
real,dimension(3,3)::a
real::sum0
real,dimension(3)::sum1,sum2
print*,'a11...a13='
read*,(a(1,j),j=1,3)
print*,'a21...a23='
read*,(a(2,j),j=1,3)
print*,'a31...a33='
read*,(a(3,j),j=1,3)
print*,'a='
do i=1,3
print'(1x,3f5.0)',(a(i,j),j=1,3)
end do
sum0=sum(a) !总和
sum1=sum(a,dim=1) !列之和
sum2=sum(a,dim=2) !行之和
print'(1x,7hsum(a),f5.0)',sum0
print'(1x,13hsum(a,dim=1),3f5.0)',sum1
print'(1x,13hsum(a,dim=2),3f5.0)',sum2
print*,'press any key to continue'
read*,
stop
end a11...a13=
444
545
555
a21...a23=
774
515
112
a31...a33=
564
213
232
a=
444. 545. 555.
774. 515. 112.
564. 213. 232.
sum(a),3954.
sum(a,dim=1),1782.1273. 899.
sum(a,dim=2),1544.1401.1009.
press any key to continue矩阵与向量的积
用到如下表现:
a(i, k: m) !矩阵a的第i行的第k到第m个元素
a(i, k: m: 2) !矩阵a的第i行的第k到第m个元素,递增量为2
a(i, :) !矩阵a的第i行
a(:, j) !矩阵a的第j列Matrix × Column Vector
program matrix
implicit none
integer, dimension(3, 3) :: a
integer, dimension(3) :: u = (/5,8,2/), v
a = reshape((/4,5,8,7,4,1,5,6,2/), (/3, 3/))
v = matmul(a, u)
print '(1x, 3i6)', v
print *,'press any key to continue'
read *,
stop
end 86 69 52
press any key to continueTwo-dimensional Rotation
program abc
implicit none
real :: t, x, y
real, dimension(2, 2) :: a
real, dimension(2, 1) :: b, c
print *, 'x, y, t = '
read *, x, y, t
a = reshape((/cos(t), sin(t), -sin(t), cos(t)/),(/2, 2/))
c = reshape((/x, y/), (/2, 1/))
b = matmul(a, c)
print *, 'new x, new y = ', b
print *,'press any key to continue'
read *,
stop
end x, y, t =
222,333,0
new x, new y = 222.000000 333.000000
press any key to continueRow Vector × Matrix
program matrix
implicit none
integer, dimension(3, 3) :: a
integer, dimension(3) :: u = (/5,8,2/), v
a = reshape((/4,5,8,7,4,1,5,6,2/), (/3, 3/))
v = matmul(u, a)
print '(1x, 3i6)', v
print *,'press any key to continue'
read *,
stop
end 76 69 77
press any key to continueRow Vector × Column Vector
program matrix
implicit none
integer :: i
integer, dimension(3, 3) :: a
integer, dimension(3, 1) :: u
integer, dimension(1, 3) :: v
u = reshape((/2, 3, 3/),(/3, 1/))
v = reshape((/2, 3, 3/),(/1, 3/))
a = matmul(u, v)
print *, 'a = '
print '(1x, 3i6)', a
print *,'press any key to continue'
read *,
stop
end a =
4 6 6
6 9 9
6 9 9
press any key to continueGaussian-Jordan Elimination
Forward Elimination
For k = 1, 2, ..., n - 1 & j = k + 1, ..., n
akj = akj / akk
bk = bk / akk
For i = k + 1, ..., n & j = k + 1, ..., n
aij = aij - aikakj
bi = bi - aikbk
Back Subsitution
xn = bn / ann
For k = n - 1, n - 2, ..., 1
xk = bk - Σnj=k+1 akjbj
Example
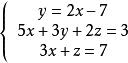
Written Calculation

Program
ATTENTION
The program provided below can only solve full rank matrices, and it is NOT accurate enough.
program gaussian_jordan
implicit none
integer, parameter :: nn = 10
integer :: i, k, kpl, n
real :: p, q
real, dimension(nn, nn) :: a
real, dimension(nn) :: b, x
!input
print *, 'n = '
read *, n
print '(1x, 25hEnter_an_Augmented_Matrix)'
do i = 1, n
read *, a(i, 1: n), b(i)
end do
!forward elimination
do k = 1, n - 1
kpl = k + 1
p = a(k, k)
a(k, kpl: n) = a(k, kpl: n) / p !affecting accuracy
b(k) = b(k) / p !affecting accuracy
do i = kpl, n
q=a(i, k)
a(i, k + 1: n) = a(i, kpl: n) - q * a(k, kpl :n)
b(i) = b(i) - q * b(k)
end do
end do
!Back Subsitution
x(n) = b(n) / a(n, n)
do k = n - 1, 1, -1
kpl = k + 1
x(k) = b(k) - dot_product(a(k, kpl: n), x(kpl: n))
end do
!output
print *, 'vector x = '
print *, x(1: n)
print *,'press any key to continue'
read *,
stop
end n =
3
Enter_an_Augmented_Matrix
-2,1,0,-7
5,3,2,3
3,0,1,7
vector x =
1.99999988 -3.00000024 1.00000012
press any key to continue